How to Calculate the Area of Irregular Shapes
Our minds are obsessed with perfect shapes and geometry. In everything we do, alignment and a perfect ratio are important. Our universe has different plans. Uncertainty plays a major role in many areas.
People are familiar with haphazard shapes. It’s simple to find the area and dimensions for regular shapes such as squares, rectangles, and circles. What if there are no edges or sides to an object? This article will discuss methods for calculating the area of irregular forms with examples of irregular shapes.
Regular shapes have sides that are defined with specific lengths. Polygons that have more than five sides are called irregular shapes. Polygons can be translated to many sides.
An irregular shape is a shape that has many sides and lengths that are irregular. We must find regular shapes in these shapes to calculate their area. This is done by breaking down a particular shape into multiple regular-shaped structures.
You can then break down irregular shapes into squares, triangles, etc. and use routine methods to calculate their area.
Calculation of the area
There are many ways to calculate the area for irregular shapes. Below are some methods that will give you a definitive answer.
- The given irregular polygon can be divided into regular shapes, and the combined area of each regular form can be found.
- You can also use unit squares to evaluate the area of these shapes.
- We can divide an irregular shape with curves into regular shapes and calculate its area accordingly.
Area evaluation using unit squares
This is one way to locate areas with irregular shapes and curves. Although the method is straightforward, it doesn’t work for perfect circles or semicircles. This method does not apply to irregular quadrilaterals. This method requires you to create a chart that has squares of equal dimension.
This means that all unit squares must have the same area. The next step is to superimpose the irregular shape onto this chart. You will find that some parts of the irregular shape will be in perfect squares and others will only take up a portion of the square.
If there is four squares of perfect occupancy and four quarters of vacant, then the area would be six square centimetres.
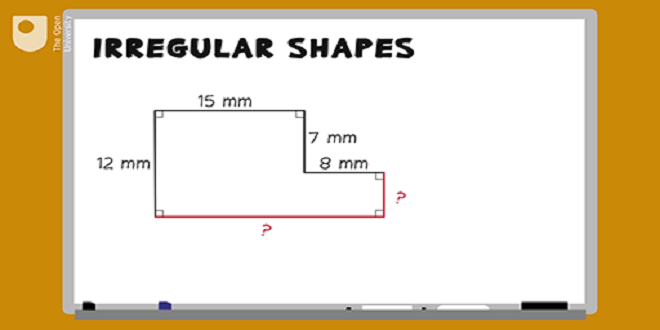
Evaluation of area for irregular shapes with square edges
Some irregular shapes, as we discussed previously, were not included in the unit square evaluation. We have therefore developed a method to divide irregular shapes with curved edges in one or more regular shapes.
Next, calculate the area for each regular shape separately. To get the final answer, each calculation must be added together.
Evaluation of area for irregular shapes with curved edges
This is the same process that’s used to evaluate such shapes for area. We then divide the irregular polygon into one of several regular shapes. If the shape has a circular edge, we add a diameter to complete the circle.
If you get rectangles, squares, triangles or semicircles at the end, first calculate each area and then add them all together to arrive at your final answer. Half of?R2 would be used to calculate a semicircle. R is the radius of your semicircle. It is also half of its diameter.
Similar to the above, you can use the following method to calculate the area of a triangle. base X perpendicular. Draw a perpendicular starting at the base median if the triangle isn’t right-angled.
Use the Pythagoras Theorem to calculate the length of your perpendicular. The area calculation for squares and rectangles can be done very easily. If you want to square a square, you will need to determine the product of length (or breadth) and width (or both). Sum up all areas and you will get your answer.
Area evaluation using graph
Some objects are not compatible with linear calculation. We need to find complex solutions for such objects.
- A leaf is one example of such an object. The laws of polygons do not apply to the leaf. To find the area, we will draw the leaf on graph paper.
- Once you’ve figured out the edges and copied the graph paper leaf, it’s time to move on to the next step.
- Next, count the squares that each leaf occupies. There will be squares that have complete occupancy and others with partial occupancy, it is obvious.
- This is because a square with more than 50% occupancy will be counted as a single unit square.
- You will begin by counting the squares. Next, find squares that have more than half occupancy.
Add these squares together to get your total. The squares that have less than half occupancy are now considered zero. The sum of squares with full occupancy and squares with less than half occupancy would give us the final answer.
Conclusion
We’ve covered all methods of calculating the area of irregular shapes in detail. To improve your skills, practice complex problems using the principles.
This basic mensuration is used in many competitive exams. You should be cautious when answering such questions. Also, remember the formula to calculate area for different shapes.
Most Frequently Asked Questions
- What are irregular shapes?
Irregular forms are polygons of irregular length. These shapes don’t have equal angles or sides.
- How do you calculate the area for irregular shapes?
We first divide irregular shapes into regular shapes and draw imaginary edges to calculate their area. To conclude, we add the area of each regular shape together.
- What applications can area evaluation methods for irregular shapes be used for?
These methods have many applications in architecture. These methods are also used in other industries, such as interior design, map drawing, and marking up agricultural fields.




